Gottfried Wilhelm Leibniz
Gottfried Wilhelm Leibniz (1646–1716) was one of the great thinkers of the seventeenth and eighteenth centuries and is known as the last “universal genius”. He made deep and important contributions to the fields of metaphysics, epistemology, logic, philosophy of religion, as well as mathematics, physics, geology, jurisprudence, and history. Even the eighteenth-century French atheist and materialist Denis Diderot, whose views were very often at odds with those of Leibniz, could not help being awed by his achievement, writing in his entry on Leibniz in the Encyclopedia, “Perhaps never has a man read as much, studied as much, meditated more, and written more than Leibniz… What he has composed on the world, God, nature, and the soul is of the most sublime eloquence. If his ideas had been expressed with the flair of Plato, the philosopher of Leipzig would cede nothing to the philosopher of Athens” (Oeuvres complètes, vol. 7, p. 709). Indeed, Diderot was almost moved to despair in this piece: “When one compares the talents one has with those of a Leibniz, one is tempted to throw away one's books and go die quietly in the dark of some forgotten corner” (Oeuvres complètes, vol. 7, p. 678). More than a century later, Gottlob Frege, who fortunately did not cast his books away in despair, expressed similar admiration, declaring that “in his writings, Leibniz threw out such a profusion of seeds of ideas that in this respect he is virtually in a class of his own” (“Boole's logical Calculus and the Concept-script” in Posthumous Writings, p. 9). The aim of this entry is primarily to introduce Leibniz's life and summarize and explicate his views in the realms of metaphysics, epistemology, and philosophical theology.
Note that throughout this entry, the following standard abbreviations are used: PC (Principle of Contradiction), PSR (Principle of Sufficient Reason), PII (Principle of the Identity of Indiscernibles), PIN (Predicate-in-Notion Principle), and CIC (Complete Individual Concept).
- 1. Life
- 2. Overview of Leibniz's Philosophy
- 3. Some Fundamental Principles of Leibniz's Philosophy
- 4. Metaphysics: A Primer on Substance
- 5. Metaphysics: Leibnizian Idealism
- 6. Epistemology
- 7. Philosophical Theology
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. Life
Leibniz was born in Leipzig on July 1, 1646, two years prior to the end of the Thirty Years War, which had ravaged central Europe. His family was Lutheran and belonged to the educated elite on both sides: his father, Friedrich Leibniz, was a jurist and professor of Moral Philosophy at the University of Leipzig, and his mother, Catharina Schmuck, the daughter of a professor of Law. Leibniz's father died in 1652, and his subsequent education was directed by his mother, uncle, and according to his own reports, himself. He was given access to his father's extensive library at a young age and proceeded to pore over its contents, particularly the volumes of ancient history and the Church Fathers.
In 1661 Leibniz began his formal university education at the University of Leipzig. As the “modern” philosophy of Descartes, Galileo, Gassendi, Hobbes and others had not made a great impact by this time in the German-speaking lands, Leibniz's philosophical education was chiefly Scholastic in its nature, though he was also exposed to elements of Renaissance humanism. While in Leipzig, Leibniz met Jacob Thomasius, who would have an important influence on Leibniz and who supervised Leibniz's first philosophical treatise On the Principle of Individuation (De principio individui). It was Thomasius more than anyone else perhaps who instilled in Leibniz a great respect for ancient and medieval philosophy. Indeed, one of the leitmotifs of Leibniz's philosophical career is his desire to reconcile the modern philosophy with the philosophy of Aristotle, Plato, the Scholastics and the Renaissance humanist tradition. After receiving his baccalaureate from Leipzig, he continued his studies at the University of Altdorf. While there Leibniz published in 1666 the remarkably original Dissertation on the Art of Combinations (Dissertatio de arte combinatoria), a work that sketched a plan for a “universal characteristic” and logical calculus, a subject that would occupy him for much of the rest of his life. Although Leibniz was offered a position on the faculty of Law upon the completion of his Doctorate of Law in 1667, he had a different future in mind.
In that year, Leibniz met Baron Johann Christian von Boineburg, a Protestant convert to Catholicism, who was able to secure a position for Leibniz with the Elector of Mainz. While in the court of the Elector, Leibniz composed a series of works in philosophical theology, the Catholic Demonstrations, which are another manifestation of Leibniz's lifelong irenicism: in this case, in their attempt to provide a basis and justification for the reconciliation of Protestantism and Catholicism. Leibniz also turned his mind to natural philosophy, having finally been able to study some of the works of the moderns; the result was a two-part treatise in 1671, the New Physical Hypothesis (Hypothesis physica nova). The first part, the Theory of Abstract Motion (Theoria motus abstracti), was dedicated to the Académie des Sciences de Paris, and the second part, the Theory of Concrete Motion (Theoria motus concreti), was dedicated to the Royal Society in London. These works, however, were not likely to impress their audiences, for, given his circumstances, Leibniz could not but produce amateurish works in the field.
This changed, however, in 1672, when Leibniz was given the single most important opportunity of his life: the Elector of Mainz sent him on a diplomatic mission to Paris, the center of learning and science at the time. Leibniz was able to stay in Paris for four years (with a brief trip to London in 1673), during which time he met many of the major figures of the intellectual world, among them Antoine Arnauld, Nicholas Malebranche, and, most important, the Dutch mathematician and physicist, Christiaan Huygens. It was he, “the great Huygenius” (as John Locke would call him in the Dedicatory Epistle to his Essay Concerning Human Understanding), who took Leibniz under his wing and tutored him in the developments in philosophy, physics, and mathematics. Not only was Leibniz able to converse with some of the greatest minds of the seventeenth century while in Paris, he was also given access to the unpublished manuscripts of Descartes and Pascal. And, according to Leibniz, it was while reading the mathematical manuscripts of Pascal that he began to conceive what would eventually become his differential calculus and his work on infinite series. In this time, Leibniz also designed a calculating machine able to perform addition, subtraction, multiplication, and division (see the Other Internet Resources for a picture). And his trip to London in 1673 was meant in part to present his designs to the Royal Society.
While Leibniz was living the life of the mind in Paris, his employer died, and Leibniz was thus forced to look for another position. He eventually found one as the librarian for Duke Johann Friedrich of Brunswick, who ruled in Hanover. On the way to Hanover, Leibniz stopped in Amsterdam to meet with Spinoza between November 18 and 21, 1676, three months before the latter's death; according to Leibniz's own notes, they spoke of Spinoza's yet-to-be-published Ethics, Cartesian physics, and Leibniz's improved version of the ontological argument (see below). Although Leibniz would travel to Italy for a time in the late 1680s in order to conduct historical research for the House of Hanover and make many shorter trips (including to Vienna), the rest of his life was essentially spent in Hanover and its environs, working in different capacities for the court, first, for Johann Friedrich until his death in 1680, then for Johann Friedrich's brother, Ernst August (from 1680 to 1698), and finally for the latter's son, Georg Ludwig, who in 1714 would become George I of England. Leibniz's relations with Ernst August and Georg Ludwig were not as amicable as his relations with his original employer, but he was close to Sophie, the wife of Ernst August and youngest sister of Princess Elisabeth of Bohemia, with whom Descartes had an important philosophical correspondence. (Sophie was also the daughter of Elizabeth Stuart, and it is for this reason that her son became King of England.)
While Leibniz may have felt physically isolated from the intellectual scene of Europe, he did manage to stay connected through a vast network of correspondents. (Leibniz exchanged letters with over 1100 different people in the course of his life.) Despite the great demands placed on Leibniz as librarian, then historian, and Privy Councillor at the court of Hanover, he was able to complete work that, in its breadth, depth, and sheer quantity, is staggering.
Leibniz's final years were bleak. He was engaged in a vituperative debate with Newton and his followers over the priority of the discovery of the calculus, even being accused of stealing Newton's ideas. (Most historians of mathematics now claim that Newton and Leibniz developed their ideas independently: Newton developing the ideas first with Leibniz the first to publish.) And at the court he was mocked for his wig and old-fashioned clothing (think 1670s Paris!). When Georg became George, the acrimony surrounding Leibniz in England was so great that Leibniz was asked to remain in Hanover rather than follow his employer to London. Leibniz died November 14, 1716.
1.1 Chronology of Major Writings
| 1684 | Meditations on Knowledge, Truth, and Ideas |
| 1686 | Discourse on Metaphysics |
| 1686f | Correspondence with Arnauld |
| 1689 | Primary Truths |
| 1695 | New System |
| 1695 | Specimen Dynamicum |
| 1697 | On the Ultimate Origination of Things |
| 1698 | On Nature Itself |
| 1699f | Correspondence with De Volder |
| 1704 | New Essays on Human Understanding |
| 1706f | Correspondence with Des Bosses |
| 1710 | Theodicy |
| 1714 | Monadology |
| 1714 | Principles of Nature and Grace |
| 1715f | Correspondence with Clarke |
2. Overview of Leibniz's Philosophy
Unlike most of the great philosophers of the period, Leibniz did not write a magnum opus; there is no single work that can be said to contain the core of his thought. While he did produce two books, the Theodicy (1710) and the New Essays Concerning Human Understanding (finished in 1704 but not published until 1765), the student of Leibniz's thought must piece together Leibniz's philosophy from his myriad writings: essays published in scholarly journals and in more popular journals; unpublished works left abandoned by their author; and his many letters. Moreover, many of Leibniz's writings have not yet been published. The authoritative scholarly version of Leibniz's works, the Akademie edition, has thus far only published his philosophical writings from 1663 to 1690; in other words, only half of his writing life has been covered. And the mere act of dating pieces often depends upon careful analysis of the paper Leibniz wrote on and watermarks and so on. (Hence, for example, the important short work, Primary Truths, which, because of its content, was often thought to date to 1686 (as in AG), has recently been redated by the Akademie editors to 1689 because of a watermark.) Piecing together Leibniz's philosophy into a systematic whole is made more difficult because Leibniz seems to have changed or at least refined his views on a number of issues over the course of his career and because he was always very aware (some might say too aware) of the audience for any of his writings.
As stated above, Leibniz's intellectual training was squarely in the tradition of Scholasticism and Renaissance humanism; his background, then, was of Aristotelianism, Platonism, and orthodox Christianity. Yet, as he became more familiar with the modern philosophy of the seventeenth century, he came to see many of its virtues. Although there is some reason to be skeptical of the details, the spirit of the self-portrait Leibniz paints to Nicolas Remond in 1714 can be a helpful guide for approaching his work. He writes:
…I have tried to uncover and unite the truth buried and scattered under the opinions of all the different philosophical sects, and I believe I have added something of my own which takes a few steps forward. The circumstances under which my studies proceeded from my earliest youth have given me some facility in this. I discovered Aristotle as a lad, and even the Scholastics did not repel me; even now I do not regret this. But then Plato too, and Plotinus, gave me some satisfaction, not to mention other ancient thinkers whom I consulted later. After finishing the trivial schools, I fell upon the moderns, and I recall walking in a grove on the outskirts of Leipzig called the Rosental, at the age of fifteen, and deliberating whether to preserve substantial forms or not. Mechanism finally prevailed and led me to apply myself to mathematics…. But when I looked for the ultimate reasons for mechanism, and even for the laws of motion, I was greatly surprised to see that they could not be found in mathematics but that I should have to return to metaphysics. This led me back to entelechies, and from the material to the formal, and at last brought me to understand, after many corrections and forward steps in my thinking, that monads or simple substances are the only true substances and that material things are only phenomena, though well founded and well connected. Of this, Plato, and even the later Academics and the skeptics too, had caught some glimpses… I flatter myself to have penetrated into the harmony of these different realms and to have seen that both sides are right provided that they do not clash with each other; that everything in nature happens mechanically and at the same time metaphysically but that the source of mechanics is metaphysics. (G III 606/L 654–55)
Again, there is some reason to doubt whether Leibniz was really fifteen when he made his philosophical perambulations and whether and to what extent he had actually read any of the moderns. Nevertheless, this self-portrait does express something that one sees in Leibniz's writings: the weaving together of varying strands of ancient and modern philosophy in a remarkably creative and sophisticated manner.
The letter to Remond makes clear that Leibniz had reservations about certain aspects of the modern philosophy, qualms that arose from and led him back to this eclectic mix of Aristotle and Christian Platonism. It is probably most helpful, then, to see Leibniz's philosophy as a reaction to two sets of modern opponents: on the one hand, Descartes and his followers; on the other hand, Hobbes and Spinoza.
Leibniz's critique of Descartes and his followers was focused principally on the Cartesian account of body or corporeal substance. According to Descartes, the essence of body is extension; that is, a corporeal substance is simply a geometric object made concrete, an object that has size and shape and is in motion. This view, indeed, is the cornerstone of the new mechanical philosophy to which Leibniz was originally attracted. Nevertheless, Leibniz came to see two distinct problems with this view. First, in claiming that the essence of body is extension, Descartes is endorsing the view that matter is infinitely divisible. But if matter is infinitely divisible, then one can never arrive at the simple unities that must exist at some ontological ground level. Second, if matter is simply extension, then there is in its nature no source of activity. If this is so, Leibniz thought, then the bodily objects of the world cannot count as substances.
Hobbes and Spinoza, despite their own differences, advanced, or were read as advancing, a number of objectionable and deeply troubling theses which Leibniz (and most of his contemporaries) saw as an enormous threat: materialism, atheism, and necessitarianism. It is Leibniz's response to Hobbesian and Spinozistic necessitarianism that is perhaps of greatest interest, for he sought to develop an account of action and contingency that would preserve divine and human freedom. As will be shown, central to Leibniz's philosophy was the view that God freely chose the best world from an infinite number of possible worlds and that a person could be said to act freely when the contrary of that action does not imply a contradiction. (This topic will be addressed principally in the article on Leibniz's Modal Metaphysics.)
3. Some Fundamental Principles of Leibniz's Philosophy
Leibniz asserts in the Monadology §§31–32, “Our reasonings are based on two great principles, that of contradiction… [and] that of sufficient reason” (G II 612/AG 217). To these two great principles could be added four more: the Principle of the Best, the Predicate-in-Notion Principle, the Principle of the Identity of Indiscernibles, and the Principle of Continuity. The relation among these principles is more complicated than one might expect. Leibniz sometimes suggests that the Principle of the Best and the Predicate-in-Notion Principle can be said to ground his “two great principles”; at other times, however, all four principles seem to work together in a system of circular implication. And while the Principle of the Identity of Indiscernibles is often presented in contemporary discussions in analytic metaphysics as a stand-alone axiom, Leibniz tells us that it follows from the two great principles. Finally, the Principle or Law of Continuity is actually a principle that Leibniz takes from his work in mathematics and applies to the infinite hierarchy of monads in the world and to the quality of their perceptions; it appears to derive only tenuous support from the Principle of Sufficient Reason.
3.1 The Principle of the Best
Leibniz presented a number of arguments for the existence of God, which represent great contributions to philosophical theology and which will be discussed below. But one of the most basic principles of his system is that God always acts for the best. While this is generally treated as an axiom, the opening of the Discourse on Metaphysics does present something of an argument for it: “God is an absolutely perfect being”; “power and knowledge are perfections, and, insofar as they belong to God, they do not have limits”; “Whence it follows that God, possessing supreme and infinite wisdom, acts in the most perfect manner, not only metaphysically, but also morally speaking…” (AG 35) This might not appear a surprising claim from a theist, but it is not obvious that God must always act for the best or even create the best world. (See Adams 1972) And Leibniz sometimes implicitly, sometimes explicitly, appeals to this principle in his metaphysics, most notably when he is also employing the Principle of Sufficient Reason. Indeed, when it comes to the creation of the world, the “sufficient reason” for God's choice of this world is that this world is the “best” of all possible worlds; in other words, in this case the Principle of Sufficient Reason is essentially the Principle of the Best.
3.2 Predicate-in-Notion Principle (PIN)
Leibniz has a very distinctive notion of truth, one which underlies much of his metaphysics. But this notion of truth goes back to Aristotle's Organon (cf. Posterior Analytics I.4), as Leibniz himself says, and it is also present in Arnauld and Nicole's Logic, or the Art of Thinking (Book IV, Chapter 6). As Leibniz puts it in a letter to Arnauld, “in every true affirmative proposition, whether necessary or contingent, universal or particular, the notion of the predicate is in some way included in that of the subject. Praedicatum inest subjecto; otherwise I do not know what truth is” (G II 56/L 337). As he tells us in the Primary Truths and the Discourse on Metaphysics, many things follow from the Predicate-in-Notion Principle (PIN), including what he believes to be the correct analysis of necessity and contingency.
3.3 Principle of Contradiction (PC)
Leibniz also follows Aristotle (cf. Metaphysics IV.3), in placing great emphasis on the Principle of Identity or the Principle of Contradiction (PC). PC states simply that “a proposition cannot be true and false at the same time, and that therefore A is A and cannot be not A” (G VI 355/AG 321). According to Leibniz, the primary truths of his metaphysical system are identities, but, in a striking move, he combines PC with PIN and asserts in Primary Truths that “all remaining truths are reduced to primary truths with the help of definitions, that is, through the resolution of notions” (A VI iv 1644/AG 31). Furthermore, the combination of PC and PIN will mean that, since in any true proposition the predicate is contained explicitly or implicitly within the subject, this is so for all affirmative truths, whether they be universal or particular, necessary or contingent. Leibniz will use this seemingly innocuous principle to draw profoundly strong metaphysical conclusions about the nature of substance and modality.
3.4 Principle of Sufficient Reason (PSR)
The Principle of Sufficient Reason (PSR) in its classic form is simply that nothing is without a reason (nihil est sine ratione) or there is no effect without a cause. As Leibniz remarks, this principle “must be considered one of the greatest and most fruitful of all human knowledge, for upon it is built a great part of metaphysics, physics, and moral science” (G VII 301/L 227). In the Principles of Nature and Grace, Leibniz suggests that the claim that nothing takes place without a sufficient reason means that nothing happens in such a way that it is impossible for someone with enough information to give a reason why it is so and not otherwise. In the Monadology and elsewhere, however, Leibniz frankly admits that “most of the time these reasons cannot be known to us” (G VI 612/AG 217). While the idea that every event must have a cause and that there is a reason why everything is so and not otherwise again might not seem novel, it is the connection that Leibniz sees between this principle and his other metaphysical principles that is noteworthy. According to Leibniz, PSR must actually follow from PIN, for if there were a truth that had no reason, then there would be a proposition whose subject did not contain the predicate, which is a violation of Leibniz's conception of truth.
3.5 Principle of the Identity of Indiscernibles (PII)
PC and PSR may seem innocent enough, but Leibniz's other well-known principle, the Principle of the Identity of Indiscernibles (PII), is more controversial. (See also the entry on identity of indiscernibles.) In one of Leibniz's typical formulations, PII states that “it is not true that two substances can resemble each other completely and differ only in number [solo numero]” (A VI, iv, 1541/AG 42). In other words, if two things share all properties, they are identical, or (∀F)(Fx ↔ Fy) → x = y. What is particularly important to note, however, is that Leibniz is adamant that certain kinds of properties are excluded from the list of properties that could count as difference-making properties, chief among these spatio-temporal properties. This is what Leibniz means (in part) when he asserts that there can be no purely extrinsic (i.e., relational) determinations. Therefore, it is not the case that there could be two chunks of matter that are qualitatively identical but existing in different locations. In Leibniz's view, any such extrinsic difference must be founded on an intrinsic difference. As he puts it in the New Essays,
although time and place (i.e., the relations to what lies outside) do distinguish for us things which we could not easily tell apart by reference to themselves alone, things are nevertheless distinguishable in themselves. Thus, although diversity in things is accompanied by diversity of time or place, time and place do not constitute the core of identity and diversity, because they [sc. different times and places] impress different states upon the thing. To which it can be added that it is by means of things that we must distinguish one time or place from another, rather than vice versa. (A VI vi 230/RB 230)
There is also the related, though uncontroversial, Principle of the Indiscernibility of Identicals: if two things are identical, then they share all properties, or x = y → (∀F)(Fx ↔ Fy). The combination of these two principles is sometimes called “Leibniz's Law”: two things are identical if and only if they share all properties, or x = y ↔ (∀F)(Fx ↔ Fy). (Sometimes, unfortunately, only the Principle of the Indiscernibility of Identicals is so called.)
It is also interesting to note that in his Primary Truths and Correspondence with Clarke, Leibniz presents PII not as a bedrock axiom of his system but as a consequence of PC and PSR. Briefly, one way to sketch the argument is this:
(1) Suppose there were two indiscernible individuals, a and b, in our world, W. (2) If this were the case, then there must also be a possible world, W*, in which a and b are “switched.” (3) But if this were the case, then God could have had no reason for choosing W over W*. (4) But God must have a reason for acting as he does. (PSR) (5) Therefore, our original supposition must be false. There are not two indiscernible individuals in our world. (PII)
Now, it was said above that Leibniz excludes purely extrinsic denominations (or relational properties) from the kinds of properties that are constitutive of an individual. To allow purely extrinsic denominations would be to accept the possibility that that two things could be discernible in terms of their relational properties while being identical in terms of their intrinsic properties, for their relational properties would not follow from their intrinsic properties. (Again, if relational properties were allowed to factor into the nature of an individual, then PII would be relatively weak. Of course two things that exist in different spatio-temporal locations are distinct, and that is what Leibniz admits in the passage from the New Essays above.) But if we follow Leibniz in excluding such relational properties as difference-making properties and reflect on the above argument, then we see that worlds are distinguished in terms of intrinsic properties of individuals and that this difference has a bearing on the relative greatness or perfection of a world. Again, let a and b be indiscernible but occupying mirror positions in W and W*. How could we ever say that W was more worthy of God's choice than W*? We could not. There must be a reason why a is here and b is there, and this reason has to do with the intrinsic properties of a and b. In other words, even the relational properties must be somehow derivative of the intrinsic properties of substances.
As we shall see, Leibniz employs this principle in a range of arguments: against the mind as a tabula rasa, against atomism, against Newtonian absolute space, and so on. (For more on this subject, consult the entry on identity of indiscernibles.)
3.6 Principle of Continuity
According to Leibniz, there are “two famous labyrinths where our reason very often goes astray” (G VI 29/H 53). The first concerns human freedom, the latter the composition of the continuum. Leibniz, however, thought that he had found the way out of each labyrinth, and his solution to the problem of the continuum is related ultimately to a maxim or law that he employs not only in his mathematical writings but also in his metaphysics. As he puts it in the Preface to the New Essays, “Nothing takes place suddenly, and it is one of my great and best confirmed maxims that nature never makes leaps” (A VI vi 56/RB 56). More exactly, Leibniz believes that this law or principle implies that any change passes through some intermediate change and that there is an actual infinity in things. The Principle of Continuity will be employed to show that no motion can arise from a state of complete rest and that “noticeable perceptions arise by degrees from ones which are too minute to be noticed” (ibid.).
4. Metaphysics: A Primer on Substance
I consider the notion of substance to be one of the keys to the true philosophy. (G III 245/AG 286)
For Leibniz, the fundamental questions of metaphysics were reducible to questions of ontology: What is there? What are the most basic components of reality? What grounds what? In a certain sense, his answer remained constant throughout his life: everything is composed of or reducible to simple substances; everything is grounded in simple substances. While Leibniz appears to have given slightly different accounts of the precise nature of these simple substances over the course of his career, there are many features that remained constant in his mature philosophy: Leibniz always believed that a substance had a “complete individual concept” and that it was essentially an active unity endowed with perception and appetition.
4.1 The Logical Conception of Substance
In §8 of the Discourse on Metaphysics, Leibniz gives one of his most important accounts of the nature of individual substance. There he claims that the Aristotelian idea that a substance is that which is the subject of predication and which cannot be predicated of something else is insufficient for a true analysis of the nature of substance. He next appeals to the PC and the PIN: in every true predication, the concept of the predicate is contained in the concept of the subject. “Since this is so,” Leibniz claims, “we can say that the nature of an individual substance or of a complete being is to have a notion so complete that it is sufficient to contain and to allow us to deduce from it all the predicates of the subject to which this notion is attributed” (A VI iv 1540/AG 41). In other words, x is a substance if and only if x has a complete individual concept (CIC), that is, a concept that contains within it all predicates of x past, present, and future. The CIC, then, serves to individuate substances; it is able to pick out its bearer from an infinity of other finite created substances. Leibniz gives as an example Alexander the Great. The concept of Alexander contains being a King, being a student of Aristotle, conquering Darius and Porus, and so on. Now, “God, seeing Alexander's individual notion or haecceity, sees in it at the same time the basis and reason for all the predicates which can be said truly of him” (A VI iv 1540–41/AG 41). Leibniz's invocation of the Scotist notion of a haecceity is intriguing. What Leibniz is telling us is that Alexander's thisness is determined by the sum of his qualitative properties. Moreover, we can see a metaphysical aspect to this logical conception of substance: the complete individual concept of a substance is the notion or essence of the substance as it known by the divine understanding.
Leibniz concludes this section with his celebrated doctrine of marks and traces: “when we consider carefully the connection of things, we can say that from all time in Alexander's soul there are vestiges of everything that has happened to him and marks of everything that will happen to him and even traces of everything that happens in the universe, even though God alone could recognize them all” (A VI iv 1541/AG 41). The doctrine of marks and traces, therefore, claims that, because the CIC contains all predicates true of a substance past, present, and future, the entire history of the universe can be read (if only by God) in the essence of any individual substance.
The consequences that Leibniz draws from the logical conception of substance and the doctrine of marks and traces are remarkable. In the following section (§9) of the Discourse on Metaphysics, we are told they include the following:
(1) No two substances can resemble each other completely and be distinct. (PII) (2) A substance can only begin in creation and end in annihilation. (3) A substance is not divisible. (4) One substance cannot be constructed from two. (5) The number of substances does not naturally increase and decrease. (6) Every substance is like a complete world and like a mirror of God or of the whole universe, which each expresses in its own way.
Unfortunately, Leibniz's reasons for drawing these consequences are not in all cases obvious. Why should PII follow from the complete individual concept account of substance? If we consider the CIC as that which allows us to pick out and individuate any individual substance from an infinity of substances, then we realize that, if the individual concepts of two substances, a and b, do not allow us (or God) to distinguish the one from the other, then their individual concepts are not complete. That is, there must always be a reason, found within the complete individual concept of substances and issuing from the free decree of God, that a is discernible from b. And this fact points to another important fact about the interpretation suggested above: it is not only the case that each substance has a complete individual concept–the essence of the substance as it exists in the divine mind–but for every essence or complete individual concept there is one and only one substance in a world. (The argument here is essentially that which was given above in the section describing the relation between PSR and PII; namely, what reason could God have had for instantiating two substances with identical CICs?) Further, why should it be the case that substances can only arise naturally in God's creation of the world and end in his annihilation? If one takes quite literally Leibniz's claim that the CIC contains within it all predicates true of the substance past, present, and future, then one might be able to say that this must include truths extending back to the creation and forward either infinitely or to the end of time. This argument might be somewhat weak in itself, but it certainly would seem to follow from Leibniz's logical notion of substance and one of the other consequences, namely, that each substance is a mirror of the entire universe. If this is the case, then a substance, insofar as it is a mirror of the entire universe, must have within its complete individual concept predicates that extend back to creation and forward in time. At first glance, it is also not readily apparent merely from the CIC and doctrine of marks and traces why a substance cannot be constructed from two substances or be divided into two new substances. Let substance x have within its complete individual concept predicates g, h, i… which are true of it past, present and future. Suppose x were to be divided into xα and xβ. One might imagine that both new substances would have all of x's pre-division predicates in common and unique predicates thereafter. But the relevant part of Leibniz's logical notion of substance is that the CIC is sufficiently rich to allow us (or God) to deduce from it all predicates past, present and future. Leibniz's implicit suggestion is that the pre-division predicates would not allow the logical deduction of branching or divided substances. If g, h, i,… imply lα, mα, nα, they cannot also imply lβ, mβ, nβ. A similar argument works against the possibility of the fusion of two substances. Further, if we already grant PII, then it should be clear that the substance having within its CIC predicates g, h, i, … lα, mα, nα, and the substance having within its CIC predicates g, h, i, … lβ, mβ, nβ are numerically distinct substances and not simply one substance in its pre-division phase that has multiplied. Since substances can only naturally arise during God's creation of the world and since substances cannot undergo fusion or fission, it is obvious that the number of substances must remain constant. Finally, if it is the case that it is of the nature of a substance to have a notion so complete that one can deduce from it all its predicates past, present, and future and if substances exist from the creation of the world, then it would seem (relatively) natural to conclude that each substance contains within it a kind of story of the entire universe from its own particular perspective. While more will be said below, what Leibniz is suggesting here is a set of doctrines that he will develop in greater detail: the worlds apart doctrine, the mirroring (or expression) thesis, and the doctrine of universal harmony.
Another notable consequence of the logical conception of substance is the denial of the causal interaction of finite substances. This is clearest in Primary Truths (C 521/L 269/AG 33), where a very similar argument concerning the nature of substance is given. Not only is it the case, Leibniz claims, that genuine physical influx – the transfer of some property within one substance to a second substance – is inexplicable, but more important the logical conception of substance shows us that the reasons for any property that a substance may have are already contained within its CIC. In other words, every state of a substance is explained, grounded, or caused by its own notion or CIC. (Of course, the ground or reason for the existence or actuality of any particular substance is to be found in God and his free choice of worlds. A more detailed account of Leibniz's views on causation is available in the entry Leibniz on Causation.) As we shall see below, the denial of the causal interaction of substances forms an essential premise of Leibniz's argument for pre-established harmony.
4.2 Unity
If a finite substance is to have a CIC, as Leibniz claims in §8 of the Discourse on Metaphysics, what is its ontological status? That is, what kind of thing could have such a CIC or such a nature? Leibniz's answer to this question brings to the fore another paradigm of substancehood: unity. While it is the nature of an individual substance to have a CIC, only a genuine unity can qualify as a substance. Leibniz expresses his position in a letter to Arnauld in a very clear and forceful manner: “To put it briefly, I hold this identical proposition, differentiated only by the emphasis, to be an axiom, namely, that what is not truly one being is not truly one being either.” (G II 97/AG 86) In the period of the Discourse on Metaphysics and Correspondence with Arnauld, Leibniz appeals to certain Scholastic notions, chief among them, the notion of a substantial form. In later years, the Scholastic way of speaking fades away, but the fundamental idea remains the same: there must be something that guarantees or makes possible the unity of a substance, and this is the substantial form or the soul. The point Leibniz wants to make is that only a soul or a substantial form is the kind of thing that can be said to have or underlie a complete individual concept, for only a soul or substantial form is by its nature an imperishable unity. Leibniz makes this point very clear in another letter to Arnauld: “A substantial unity requires a thoroughly indivisible and naturally indestructible being, since its notion includes everything that will happen to it, something which can be found neither in shape nor in motion (both of which involve something imaginary, as I could demonstrate), but which can be found in a soul or substantial form, on the model of what is called me” (G II 76/AG 79). Thus, unity is the hallmark of a genuine substance, but equally important is Leibniz's paradigm case of a substance: the self. This thought underlies much of Leibniz's reflections on the nature of substance and has important consequences. For, following not only Descartes but also the entire Augustinian tradition, the “I” is essentially immaterial, a mind or a soul. Similarly, he writes in Primary Truths, “Something lacking extension is required for the substance of bodies, otherwise there would be no source [principium] for the reality of phenomena or for true unity… But since atoms are excluded, what remains is something lacking extension, analogous to the soul, which they once called form or species” (A VI iv 1648/AG 34). (Material atoms, as advocated by Democritus in the classical period and by Gassendi and others in the seventeenth century, are excluded, Leibniz thinks, because they violate PII; that is, two purely material atoms would seem to be qualitatively identical and yet distinct, which is impossible if one accepts PC, PSR, and the derivation of PII.)
Leibniz is not as clear as one would like him to be, for at this point in his career it is possible to read him as seeing that something is a substance so long as it has a soul or a substantial form, whereas later in his career it seems more clearly to be the case that the only substances are souls or soul-like entities, the monads. In other words, Leibniz can be interpreted as advocating, at least in this period, a kind of Aristotelian hylomorphism, in which substances are composites of matter and form. This has been the subject of debate in the field, but this entry cannot adjudicate the matter. (For more on this dispute, see Look 2010.)
Nevertheless, in declaring that a substance is necessarily indivisible, Leibniz renders it impossible for a body, or matter alone, to be a substance. Thus, Cartesian corporeal substance, the essence of which is simply extension, cannot exist as substance. Put differently, Leibniz's argument is that nothing that is divisible is a substance; a Cartesian chunk of matter is divisible; therefore, a Cartesian chunk of matter is not a substance. This points to the first part of Leibniz's critique of the Cartesianism mentioned above: namely, that according to Leibniz, Cartesian matter fails to have the unity required of a genuine substance. Indeed, in the Correspondence with Arnauld, Leibniz considers the case of a human body deprived of a soul and says the body, or cadaver, would not be a substance at all but merely an aggregate of substances. Moreover, anything lacking a substantial form or soul is not a substance, that is, if a thing is not truly “animated”, then it is only a true phenomenon. (G II 77/AG 80) It should be noted how strong Leibniz's claim is: he is arguing that Cartesian corporeal substances or any such chunks of matter are not real beings – at least not as real as simple substances. Aggregates of simple substances, therefore, have a different ontological status from simple substances.
The distinction between simple substances and aggregates becomes an important one in Leibniz's philosophy. To Arnauld, he writes the following: “I hold that philosophy cannot be better reestablished and reduced to something precise, than by recognizing only substances or complete beings endowed with a true unity, together with the different states that succeed one another; everything else is only phenomena, abstractions, or relations” (G II 101/AG 89). If this is the case, then aggregates of simple substances are merely phenomena and fail to have the reality of the underlying simples. Further, the bodies of natural philosophy, the bodies of the world we observe around us, would seem to be in some sense mere phenomena.
While some scholars of Leibniz's thought have suggested this, it does not get at the full story of Leibniz's metaphysical system. The distinction that Leibniz draws is one between a real unity and a phenomenal unity, or as he also puts it, between a unum per se and a unum per aggregationem. Leibniz's favorite comparison in the case of the latter is to a rainbow: bodies, for example, fail to have intrinsic unity, but we do represent them as being single and unified objects much as we represent a rainbow as being one thing when it is in fact merely the result of the refraction of light through innumerable water droplets. But just as the rainbow results from the presence of genuine unities, the water droplets (to continue the metaphor, even if this is not true when speaking with Leibniz in metaphysical rigor), so do the bodies of the natural world result from the genuine simple substances. Put differently, the simple substances ground the phenomena of bodies in the world. This relation between the phenomena and the underlying simple substances is what Leibniz means when he talks about “well-founded phenomena” [phenomena bene fundata]. But insofar as the bodies of the natural world are well-founded phenomena – that is, insofar as they are grounded in the simple substances – they are not simply phenomena as in Berkeley's philosophy. (This view is also not uncontroversial. To compare Leibniz with Berkeley, see the entry on Berkeley.)
4.3 Activity
The second part of Leibniz's critique of the Cartesian doctrine of corporeal substance relates to the notion of activity. According to Leibniz, substances are not only essentially unities, but also active. As he says in the opening line of the Principles of Nature and Grace: “A Substance is a being capable of action” (G VI 598/AG 207). But Cartesian corporeal substance, insofar as its essence is extension, cannot be itself a source of activity. (G IV 510/AG 161) There are at least two strands to Leibniz's argument on this point. First, Leibniz holds that this is so because he adheres to the classical and Scholastic idea that actions pertain to supposita; that is, only something that can be the subject of predication can be active, and only true unities can be genuine subjects of predication (and not mere phenomena). Put differently, Cartesian extended stuff cannot, insofar as it is infinitely divisible, constitute a suppositum, or subject of predication. But, second, Leibniz believes that something is active if and only if the source of its activity can arise within itself, that is, if and only if its activity arises spontaneously from within itself. This is another reason, then, that individual substances will be understood as mind-like, for Leibniz believes that only minds or mind-like things can originate and alter their modifications.
In saying that substances are essentially active, Leibniz means that they are endowed with forces. More precisely, according to Leibniz, “the very substance of things consists in a force for acting and being acted upon,” (G IV 508/AG 159) that is, each simple substance is endowed with what Leibniz calls primitive active and passive powers. The idea here again sounds Aristotelian: a substance has a certain essentially active component, the soul or substantial form or first entelechy, and a passive component, primary matter. In Leibniz's mature account, the primitive active force is “an inherent law, impressed by divine decree,” that is, it is the law of unfolding or the law of the series of the simple substance. As he puts it in a letter to De Volder, “I think that it is obvious that primitive forces can be nothing but the internal strivings [tendentia] of simple substances, strivings by means of which they pass from perception to perception in accordance with a certain law of their nature, and at the same time harmonize with one another, representing the same phenomena of the universe in different ways, something that must necessarily arise from a common cause” (G II 275/AG 181). Since simple substances are minds, their modifications are representations or perceptions, and the activity of the simple substance will relate to the change or succession of its perceptions. One way to think of this is that each substance has a unique series of perceptions programmed by God to play in harmony with all other substances, and the internal tendency of a substance to move from perception to perception is its active force, or what Leibniz also calls appetite or appetition.
4.4 Pre-established Harmony
While separate entries detail Leibniz's account of causation and his account of the mind, it will still be useful to provide a short exegesis of Leibniz's celebrated solution to the mind-body problem which Leibniz had inherited from Descartes and his followers. The problem, briefly, is this: if mind is essentially thought (and nothing else), and body is essentially extension, then how can mind and body interact or form a unity as we know from experience they must? Or how do thinking substance and extended substance unite in the substance of a human being? Leibniz answers this question by, first, denying the possibility of the causal interaction of finite substances. In this way, Leibniz undermines Cartesian dualism because it takes as a premise the idea that mind-body interaction is to be explained by the influence of the one on the other via the pineal gland. (See the Sixth Meditation: AT VII 86–87/CSM II 59–60) But Leibniz also saw pre-established harmony as an account of the mind-body relation that avoided the difficulties inherent in Occasionalist theories of the mind and the interaction of substances. In one of Leibniz's best-known metaphors, he asks his readers to imagine the mind and body as two pendula hanging from a beam. Whence comes their agreement? One could imagine that the motion of the one is communicated through the wooden beam to the other, thus causing them eventually to swing harmoniously (the theory of influx). Or one could imagine that God intervenes and moves the pendula, guaranteeing their synchronicity (the theory of occasionalism). Or, Leibniz says, one could imagine that God, the supreme artificer, created the world (and the pendula) so perfectly that, by their own natures, they would swing in perfect harmony. Naturally, it is this last thesis that Leibniz endorses and asks his readers to endorse as well. (See, for example, the Postscript of a Letter to Basnage de Beauval (G IV 498–500/AG 147–49).)
More precisely, Leibniz argues that God created the world so perfectly that each substance acts according to its own law of unfolding and is at the same time in perfect harmony with all others substances; further, that the mind has a distinct point of view of the world by virtue of its being the center of some mass (body), and that the law of unfolding of the mind is in accord with the laws of the corporeal machine. He puts this most succinctly in his 1695 essay, A New System of Nature, in which he effectively presents a five-step argument for pre-established harmony:
(1) “[T]here is no real influence of one created substance on another.” (G IV 483/AG 143) (2) “God originally created the soul (and any other real unity) in such a way that everything must arise for it from its own depths [fonds], through perfect spontaneity relative to itself, and yet with a perfect conformity relative to external things.” (G IV 484/AG 143) (3) “This is what makes every substance represent the whole universe exactly and in its own way, from a certain point of view, and makes the perceptions or expressions of external things occur in the soul at a given time, in virtue of its own laws, as if in a world apart, and as if there existed only God and itself.” (G IV 484/AG 143) (4) “[T]he organized mass, in which the point of view of the soul lies, being expressed more closely by the soul, is in turn ready to act by itself, following the laws of the corporeal machine, at the moment when the soul wills it to act, without disturbing the laws of the other – the spirits and blood then having exactly the motions that they need to respond to the passions and perceptions of the soul.” (G IV 484/AG 144) (5) “It is this mutual relation, regulated in advance in each substance of the universe, which produces what we call their communication, and which alone brings about the union of soul and body.” (G IV 484–85/AG 144)
Now, when Leibniz speaks in metaphysical rigor, he denies the underlying premise of Cartesian dualism: body is not a substance; so there can be no question of how it qua substance interacts with or is related to the mind, or thinking substance. Nevertheless, Leibniz was able to express his view for the vulgar – that is, for those expecting a Cartesian metaphysics – by saying that the mind and body can be said to form a union and interact insofar as the mind follows its laws, the body follows its laws, and they are in perfect harmony. The body and soul are not united to each other in the sense that Descartes had suggested, but the perceptions and appetitions of the soul will arise spontaneously from its own stores and will correspond to the actions of the body as well as to the events of the world. In other words, while the perceptions and appetitions of the mind or soul will be independent of the body, they will nevertheless correspond precisely to the actions of the particular body to which it is attached and be in perfect conformity with all the other substances of the world.
On Leibniz's view, to individual substances there belong only perceptions and appetitions, and these perceptions and appetitions can be understood to form a series within the individual substance. In other words, every individual substance can be thought to have a set of perceptions and appetitions such that one could say that, at any given time, a particular substance was experiencing such-and-such a perception and such-and-such an appetition. Indeed, Leibniz's view is that a given substance, x, has, within its individual concept, information of the following sort: x at time t1 will have perception1 and/or appetition1; x at t2 will have perception2 and/or appetition2; and so on. (In fact, the position is more complex; for, as will be shown in a subsequent section, the mind has at any moment an infinity of petites perceptions within it, perceptions of everything that is occurring in the universe, but the human mind at least will be truly aware of one thing at a time. For example, the reader of this article could be said to have a temporally-ordered series of perceptions – with t1 corresponding to the first sentence, t2 the second sentence, etc. – and also “background noise” of which the reader is not directly aware – for example, the sound of an ambulance's siren gradually approaching and retreating from t1 to t3.) Moreover, the series of perceptions and appetitions are generated from within the individual substance itself. That is, Leibniz speaks as if perceptions and appetitions follow naturally from prior perceptions and appetitions – and it is in this respect, after all, that a finite individual substance is causally independent from all other finite created substances.
The crucial idea is that the body will follow its own laws, the mind its own laws, and there will be no true influence between the two. The mind and body thus seem to constitute, as it were, worlds apart, as indeed Leibniz claims later when he explains the world in terms of monads, and these worlds apart are, according to Leibniz, unified solely by virtue of the correspondence of their actions and perceptions. Further, to these separate realms there will apply two distinct means of explaining the events of the world: we may explain things according to the final causes of the mind or according to the efficient causes of the body or of bodies in general. Thus, not only do the mind and body each seem to follow a different set of laws, but the world, according to Leibniz, can be described in terms of either set of laws.
4.5 Efficient and Final Causes and the Kingdoms of Nature and Grace
Leibniz's account of the pre-established harmony of mind and body is part of a more general position in his metaphysics: the existence of parallel modes of explanation. As we saw above, Leibniz believes that the mind will act according to its laws and the body according to its laws and the two will be in harmony. But Leibniz also believes that the mind or soul operates for particular ends and that therefore its actions are explicable in terms of final causes, whereas the actions of the body, purely instances of matter in motion according to the claims of the mechanical philosophy, are to be explained in terms of efficient causes. As he puts it in the Monadology §§79 and 81,
Souls act according to the laws of final causes, through appetitions, ends, and means. Bodies act according to the laws of efficient causes or of motions. And these two kingdoms, that of efficient causes and that of final causes, are in harmony with each other.
According to this system, bodies act as if there were no souls (though this is impossible); and souls act as if there were no bodies; and both act as if each influenced the other. (G VI 620–21/AG 223)
In the realm of natural philosophy, Leibniz will say clearly that “all corporeal phenomena can be derived from efficient and mechanical causes,” though there are final causes (or “higher reasons”) that underlie them. (See Specimen Dynamicum: GM VI 242/AG 126) But Leibniz pushes the parallelism even further:
In general, we must hold that everything in the world can be explained in two ways: through the kingdom of power, that is, through efficient causes, and through the kingdom of wisdom, that is, through final causes, through God, governing bodies for his glory, like an architect, governing them as machines that follow the laws of size or mathematics, governing them, indeed, for the use of souls, and through God governing for his glory souls capable of wisdom, governing them as his fellow citizens, members with him of a certain society, governing them like a prince, indeed like a father, through laws of goodness or moral laws. (GM VI 243/AG 126)
Though Leibniz speaks here of the kingdoms of power and wisdom, the two-tiered explanatory approach – the phenomena of the natural world explained through efficient causes and the actions of the mind explained through final causes – leads to the distinction between what he more commonly calls the kingdom of nature and the kingdom of grace. (See Monadology §87) Thus, on Leibniz's view, we can understand the world as if designed by God, the perfect engineer or architect, and we can also understand the world as if ordered and guided by God, the supreme monarch, who is concerned solely with the happiness of his subjects.
5. Metaphysics: Leibnizian Idealism
5.1 Monads and the World of Phenomena
Thus far we have seen that Leibniz rejected the Cartesian account of matter, according to which matter, the essence of which is extension, could be considered a substance. Leibniz held instead that only beings endowed with true unity and capable of action can count as substances. The ultimate expression of Leibniz's view comes in his celebrated theory of monads, in which the only beings that will count as genuine substances and hence be considered real are mind-like simple substances endowed with perception and appetite. What was said above concerning the unity and activity of simple substance should suffice to explain Leibniz's reasons for holding such a position. Now a fuller version of Leibniz's idealism must be presented.
According to Leibniz, if the only genuinely real beings are mind-like simple substances, then bodies, motion, and everything else must result from or be derivative of those simple substances and their perceptual states. In a typical statement of his idealism, Leibniz says, “I don't really eliminate body, but reduce [revoco] it to what it is. For I show that corporeal mass [massa], which is thought to have something over and above simple substances, is not a substance, but a phenomenon resulting from simple substances, which alone have unity and absolute reality” (G II 275/AG 181). Yet, this position, denying the reality of bodies and asserting that monads are the grounds of all corporeal phenomena, as well as its metaphysical corollaries has shocked many. Bertrand Russell, for example, famously remarked in the Preface to his book on Leibniz that he felt that “the Monadology was a kind of fantastic fairy tale, coherent perhaps, but wholly arbitrary.” And, in perhaps the wittiest and most biting rhetorical question asked of Leibniz, Voltaire gibes, “Can you really believe that a drop of urine is an infinity of monads, and that each of these has ideas, however obscure, of the universe as a whole?” (Oeuvres complètes, Vol. 22, p. 434) Well, if you are Leibniz, you can. But how so?
5.2 Panorganicism and Idealism
When Leibniz argues that bodies are the results of monads and that matter itself is a phenomenon, he has something very specific in mind. First, in Leibniz's system there is a special kind of order in the natural world corresponding to a hierarchy of monads. Consider first a well-known comment that Leibniz makes to De Volder, introducing a five-fold ontological scheme: “I distinguish: (1) the primitive entelechy or soul; (2) the matter, namely, the primary matter or primitive passive power; (3) the monad made up of these two things; (4) the mass [massa] or secondary matter, or the organic machine in which innumerable subordinate monads come together; and (5) the animal, that is, the corporeal substance, which the dominating monad makes into one machine” (G II 252/AG 177). One of the points Leibniz is making here is that in an animal there is a dominant monad that bears a special relation to all the monads subordinate to it that make the “organic machine” of that animal. But, ultimately, the picture is even more complex than this, for each of the subordinate monads can be considered as having an organic machine attached to it, and this relation continues on to the infinitely small. Thus, for example, Leibniz writes in the Monadology §70, “Thus we see that each living body has a dominant entelechy, which in the animal is the soul; but the limbs of this living body are full of other living beings, plants, animals, each of which also has its entelechy, or its dominant soul” (G VI 619/AG 222). Similarly, in a letter to Bierling, he writes, “Any mass contains innumerable monads, for although any one organic body in nature has its corresponding [dominant] monad, it nevertheless contains in its parts other monads endowed in the same way with organic bodies subservient to the primary one; and the whole of nature is nothing else, for it is necessary that every aggregate result from simple substances as if from elements” (G VII 502). In other words, each monad will have an organic body which is in turn composed of other monads, each of which likewise has an organic body. Similarly, any seemingly inanimate chunk of matter – a stone or, yes, a drop of urine – will be the result of an infinity of monads and their organic bodies, which are nothing more than more monads and their organic bodies. This view is associated with a panorganicist strand of Leibniz's thought. And it is for this reason that Leibniz will claim that “all of nature is full of life” (Principles of Nature and Grace §1: G VI 598/AG 207) and that “there are infinite degrees of life in the monads” (Principles of Nature and Grace §4: G VI 599/AG 208).
Second, there is what can best be described as a genuinely idealist strand of Leibniz's thought. That is, if idealism is the thesis that the only things that truly exist are minds and their ideas, then Leibniz clearly espouses this doctrine. Here the operative idea is that bodies, and in particular the bodies associated with particular minds, are intentional objects – though they result from or are grounded in monads. This is what Leibniz is getting at in the following passage from another letter to De Volder: “considering the matter carefully, we must say that there is nothing in things but simple substances, and in them, perception and appetition. Moreover, matter and motion are not substances or things as much as they are the phenomena of perceivers, the reality of which is situated in the harmony of the perceivers with themselves (at different times) and with other perceivers” (G II 270/AG 181). Thus, the only real things are simple substances; the bodies that we perceive in motion around us are phenomena and not themselves substances, though they are grounded ultimately in simple substances or monads. Furthermore, the bodies of the natural world ought be considered intentional objects in that they are objects about which we have certain beliefs. This is what Leibniz means in saying that they have reality insofar as there is a harmony between perceivers or between the same perceivers' beliefs or perceptions at different times. In other words, one's body or even a stone is real because it is an object of perception that fits into an account of the world that is both coherent from the point of view of the single perceiver and in harmony with the perceptions of other minds.
5.3 Perspective and Divine Emanation
Still Leibniz's version of idealism tends to produce confusion precisely because of these two strands: the commitment to the “embodiment” of monads along with the rejection of the reality of bodies; the view that monads are not spatial but have a point of view. Leibniz's point, however, is that, while monads are not extended, they do have a situation insofar as they bear an ordered relation to other bodies through the body in which they are present or through the body to which they represent themselves as being attached. (G II 253/AG 178) In other words, in the Leibnizian monadology, simple substances are mind-like entities that do not, strictly speaking, exist in space but that represent the universe from a unique perspective.
Leibniz's conception of such a perspectival universe has, however, a distinctively Platonist origin. Again, each mind-like simple substance represents itself as having a body and a position relative to other bodies, but in doing so each simple substance offers a perspective on the world for the divine mind. This idea comes out very clearly in the Discourse on Metaphysics §14, where Leibniz writes the following:
Now, first of all, it is very evident that created substances depend upon God, who preserves them and who even produces them continually by a kind of emanation, just as we produce our thoughts. For God, so to speak, turns on all sides and in all ways the general system of phenomena which he finds it good to produce in order to manifest his glory, and he views all the faces of the world in all ways possible, since there is no relation that escapes his omniscience. The result of each view of the universe, as seen from a certain position, is a substance which expresses the universe in conformity with this view, should God see fit to render his thought actual and to produce this substance. (A VI iv 1549–50/AG 46–47)
This is a striking passage. Leibniz is telling us that each finite substance is the result of a different perspective that God can take of the universe and that each created substance is an emanation of God. The argument here can be expressed in several different ways. First, since God could occupy any and all points of view of the universe, there must be a simple substance to represent the world from that perspective. (And since the simple substance must have representations of its unique perspective, it must be a mind-like substance, a monad, capable of having perceptions.) Second, and stronger, God's omniscience entails knowledge of the world from every perspective simultaneously, and the infinite perspectives of the world originating from God's nature simply are monads.
5.4 Monadic Hierarchies
If the only things that truly exist are mind-like entities, monads, then the differences between them must be explicable in terms of mental features. Now, it was stated above that a central feature of Leibniz's account of substance was his claim that substances are endowed with active and passive forces. In his mature metaphysics, Leibniz expresses this view somewhat differently by saying that a substance is active insofar as it has distinct perceptions and passive insofar as it has confused perceptions. Thus, for example, in §49 of the Monadology, Leibniz writes that, “we attribute action to a monad insofar as it has distinct perceptions, and passion, insofar as it has confused perceptions” (G VI 615/AG 219). But, as we learn later in the same work, “Monads all go confusedly to infinity, to the whole; but they are limited and differentiated by the degrees of their distinct perceptions” (G VI 617/AG 221). The fundamental idea here is two-fold: first, activity and passivity are features of the relative clarity and distinctness of the representations of the monad, and, second, insofar as the organic bodies of a particular monad are themselves constituted by monads, they – the monads of the organic body – will have confused perceptions. This chain goes down to the infinitely small, with monads having only very confused and inexact perceptions of the world.
Since there is a hierarchy among monads within any animal, from the soul of a person down to the infinitely small monad, the relation of domination and subordination among monads is a crucial feature of both Leibniz's idealism and his panorganicism. But the hierarchy of substances is not simply one of containment, in which one monad has an organic body which is the result of other monads, each of which has an organic body, and so on. In the case of animals (brutes and human beings), the hierarchy of monads is also related to the control of the “machine of nature” (as Leibniz had put it in a letter to De Volder considered above). What is it then that explains the relation of dominant and subordinate monads? As Leibniz tells Des Bosses, domination and subordination consists of degrees of perfection. Since monads are to be differentiated in terms of their perceptions, one natural reading would simply be that suggested in the paragraph above: monad x is dominant over monad y when x has clearer perceptions than y. But, if we follow the description of the appearance of causal interaction that we find in the Monadology (§§49–51), we can get a slightly more sophisticated picture. Monad x is dominant over monad y when x contains within it reasons for the actions of y. This is why the mind of an animal can be said to direct the actions of its body, and why, for example, there will be a hierarchy of functionality within any one animal. Thus, one's mind has clearer perceptions than those contained in the monads of its organic body, but it contains the reasons for everything that happens in one's body; one's liver contains the reasons for what happens in its cells; a cell contains the reasons for what happens in its mitochondria; and, according to Leibniz, this relation continues infinitely on down.
6. Epistemology
Leibniz's reflections on epistemological matters do not rival his reflections on logic, metaphysics, divine justice, and natural philosophy in terms of quantity. Nevertheless, he did think deeply about the possibility and nature of human knowledge, and his main doctrines will be presented here.
6.1 “Meditations on Knowledge, Truth, and Ideas”
In 1684, Leibniz published a short treatise with the above title. It was his first mature publication and one to which he often referred in the course of his philosophical career. In it, Leibniz sets out a series of distinctions for human knowledge or cognition (cognitio): knowledge is either obscure or clear; clear knowledge is either confused or distinct; distinct knowledge is either inadequate or adequate; and adequate knowledge is either symbolic or intuitive. Now, according to Leibniz, clear knowledge means being able to recognize something that is represented to us, for example, a rose; and knowledge is both clear and distinct when one can enumerate marks sufficient to distinguish a rose from other things. When one can give such an enumeration, one possesses a distinct notion or concept and is thus able to give a nominal definition of the thing. Further, if all the marks that form part of a distinct notion are themselves distinctly known, then the cognition is adequate. And, finally, if a notion is complex and we are able to consider all its component notions simultaneously, then our knowledge of it is intuitive. Ultimately, Leibniz holds that human beings have intuitive knowledge only of primary notions and propositions, whereas God, of course, has intuitive knowledge of all things.
Leibniz believes his distinctions also serve to show the difference between true and false ideas. “An idea is true,” he writes, “when its notion is possible and false when it includes a contradiction” (A VI iv 589/AG 26). Now, possibility can be established a priori and a posteriori. On the one hand, we can know a priori that something is possible if we can resolve it into its component notions which are themselves possible and if we know that there is no incompatibility among those component notions. On the other hand, we know a posteriori that something is possible merely through experience, for the actual existence of a thing is proof of its possibility.
6.2 Truths of Reason and Truths of Fact
While Leibniz's Principle of Contradiction and Principle of Sufficient Reason were discussed above, it was not mentioned that these two principles are employed in the service of Leibniz's distinction between truths of reasoning and truths of fact, that is, between necessary truths and contingent truths. Leibniz's account of modality is treated elsewhere, but a short account of this distinction is here required. In the case of a truth of reasoning, its reason or explanation can be discovered by analysis of the notions or concepts, “resolving it into simpler ideas and simpler truths until we reach the primitives” (G VI 612/AG 217). Ultimately, all truths of reasoning will be resolvable into primitives or identities, and the Principle of Contradiction is thereby operative. In the case of a truth of fact, on the other hand, its reason cannot be discovered through a finite process of analysis or resolution of notions. However, there must be a reason that some particular fact is so and not otherwise (PSR), and, according to Leibniz, this reason is found outside the series of contingent things. (See below.)
6.3 Innate Ideas
Leibniz is often put in the camp of rationalists and opposed to the empiricists (for example, Locke, Berkeley, and Hume). While there are good grounds to be unhappy with this standard textbook distinction, Leibniz does fit the bill in two important respects: he is a rationalist insofar as he holds to the Principle of Sufficient Reason, and he is a rationalist insofar as he accepts innate ideas and denies that the mind is at birth a tabula rasa or blank slate. In terms of Leibniz's classical allegiances, it is interesting to see that in the realm of metaphysics, he often couched his philosophy in Aristotelian (and Scholastic) terms but that in the realm of epistemology, he was a fairly open Platonist – at least in terms of the existence of innate ideas. Indeed, in the opening passages of his New Essays on Human Understanding, his book-length commentary on Locke's Essay Concerning Human Understanding, Leibniz explicitly aligns himself with Plato on the fundamental question of the origin of ideas. (A VI vi 48/RB 48)
Leibniz has several straightforwardly metaphysical reasons for denying that the mind could be a tabula rasa. First, and most obvious, since there can be no genuine causal interaction among substances, then there could be no way that all our ideas could come from experience; indeed, no ideas could, strictly speaking, come from experience. (Leibniz will, however, adopt a more liberal understanding of sense experience, so that this is not mooted tout court.) But, second, and rarely remarked upon, Leibniz believes that the view that our minds are blank slates at birth violates the Principle of the Identity of Indiscernibles. In short, PII works against qualitatively identical physical atoms and against qualitatively identical (because blank) souls. Further, in one telling passage, he shows us the metaphysical underpinnings of the empiricist view that he finds so objectionable. He writes, “Experience is necessary, I admit, if the soul is to be given such and such thoughts, and if it is to take heed of the ideas that are within us. But how could experience and the senses provide the ideas? Does the soul have windows? Is it similar to writing-tablets, or like wax? Clearly, those who take this view of the soul are treating it as fundamentally corporeal” (A VI vi 110/RB 110). Locke famously entertained the possibility of “thinking matter”, and Leibniz found such a thesis abhorrent. Throughout his career, Leibniz expresses no doubt that the human mind or soul is essentially immaterial, and Locke's skepticism about the nature of substance is fundamentally at odds with Leibniz's most deeply held philosophical commitments. But, of course, the consequence of this is that Leibniz seeks to undermine Locke's position with respect to the origin and nature of ideas. That the mind, according to Leibniz, must be essentially immaterial has been shown above in the section on metaphysics. But Leibniz does have a particular argument for the mind's immateriality or against its mechanism that concerns the nature of thought and ideas. This is his famous metaphor of a mill, which comes forth both in the New Essays and the Monadology. According to Leibniz, perceptions cannot be explained in mechanical or materialistic terms. Even if one were to create a machine to which one attributes thought and the presence of perceptions, inspection of the interior of this machine would not show the experience of thoughts or perceptions, only the motions of various parts.
But even when Leibniz accepts the common way of speaking – that is, as if the senses are causally responsible for some ideas – he has arguments against the empiricist claim that the senses are the origin of all ideas. According to Leibniz, while the empiricist position can explain the source of contingent truths, it cannot adequately explain the origin and character of necessary truths. For the senses could never arrive at the universality of any necessary truth; they can, at best, provide us with the means of making a relatively strong induction. Rather, it is the understanding itself, Leibniz claims, which is the source of such truths and which guarantees their very necessity. While we are not aware of all our ideas at any time – a fact demonstrated by the function and role of memory – certain ideas or truths are in our minds as dispositions or tendencies. This is what is meant by an innate idea or an innate truth. Indeed, Leibniz believes that the mind has a “special affinity” for necessary truths. On this subject, Leibniz uses a distinctive metaphor: a piece of marble has veins that indicate or are disposed to indicate shapes that a skillful sculptor can discover and exploit. Similarly, there is a “disposition, an aptitude, a preformation, which determines our soul and brings it about that [necessary truths] are derivable from it” (A VI vi 80/RB 80).
6.4 Apperception, Memory, and Reason
The hierarchy of monads mentioned above has a corollary in Leibniz's epistemology. Monads are more or less perfect depending upon the clarity of their perceptions, and a monad is dominant over another when the one contains reasons for what happens in the other. But some monads can also rise to the level of souls when, for example, they experience sensations, that is, when their perceptions are very distinct and accompanied by memory. This is a position occupied by animals. Furthermore, some souls are sometimes also in a position to engage in apperception, that is, to reflect on their inner states or perceptions. As Leibniz tells us in the Principles of Nature and Grace, “it is good to distinguish between perception, which is the internal state of the monad representing external things, and apperception, which is consciousness, or the reflective knowledge of this internal state, something not given to all souls, nor at all times to a given soul” (G VI 600/AG 208). The point that Leibniz wants to make is clearly an anti-Cartesian one: it is not the case that animals lack souls and are mere machines. There is a continuum here from God, angels, and human beings through animals to stones and the dull monads which underlie the muck and grime of the world; and this continuum is not solely to be understood in terms of the comparative clarity of the mind's perceptions but also in terms of the kinds of mental activity possible for a particular being. Indeed, according to Leibniz, animals operate not as mere automata as they do in the Cartesian philosophy, but rather have fairly sophisticated mental faculties. Even a dog, for example, is capable, by virtue of its memory, of having a perception of a prior perception: “[t]hat is why a dog runs away from the stick with which he was beaten, because his memory represents to him the pain which the stick caused him” (G VI 600/AG 208). While this resembles reasoning, it is not the kind of reasoning that human beings are capable of; for the mental processes of the dog are “only founded in the memory of facts or effects, and not at all in the knowledge of causes” (ibid.). At the same time, Leibniz is quick to add that the mental activity of the dog is the same as the mental activity of human beings in three fourths of their actions, for most of us most of the time are not actually reasoning from causes to effects. And yet we are different from the beasts, Leibniz believes. Some creatures are capable of knowing the necessary and eternal truths of logic and mathematics and a priori truths (from cause to effect), and they “are properly called rational animals, and their souls are called minds.” (G VI 601/AG 209) As Leibniz says, “These souls are capable of performing reflective acts, and capable of considering what is called ”I“, substance, soul, mind – in brief, immaterial things and immaterial truths. And that is what makes us capable of the sciences of demonstrative knowledge” (ibid.). Thus, what makes human beings (and higher minds) special is the capacity, via apperception, to formulate a conception of the self. Indeed, as we see in this passage, Leibniz suggests that rationality itself follows from the capacity for reflection: we begin with a conception of the self; we move from this point to thinking of being, of substance, of God; and we become aware as well of eternal and necessary truths. Rationality, however, is really only the ability to form “indubitable connection[s] of ideas” and to follow them to their “infallible consequences” (ibid.). In other words, animals and most human beings most of the time are purely empiricists; a rational person, however, is one who can engage in genuine a priori reasoning, moving from knowledge of a true cause via deduction to necessary effects.
6.5 Petites Perceptions
One of the fundamental theses of Leibniz's philosophy is that each substance expresses the entire universe. In order to incorporate this thesis into his general epistemology and philosophy of mind, Leibniz develops his account of “petites perceptions” or “minute perceptions” mentioned briefly in the section on pre-established harmony. As he puts it in the Preface to the New Essays, “at every moment there is in us an infinity of perceptions, unaccompanied by awareness or reflection; that is, of alterations in the soul itself, of which we are unaware because these impressions are either too minute and too numerous, or else too unvarying, so that they are not sufficiently distinctive on their own” (A VI vi 53/RB 53). In other words, everything that takes place in the universe really is expressed by each finite mind, but the infinite perceptions present in the mind – from the butterfly's flight in the Amazonian jungle to the penguin's waddling in Antarctica – are usually too minute or too indistinct to outweigh, for example, the appearance of this computer screen or the feeling of hunger. Indeed, this infinity of perceptions is likened by Leibniz to the roar of the sea. “To hear this noise as we do,” Leibniz says, “we must hear the parts which make up this whole, that is the noise of each wave, although each of these little noises makes itself known only when combined confusedly with all the others, and would not be noticed if the wave which made it were by itself” (A VI vi 54/RB 54). The infinity of petites perceptions is, then, simply epistemological white noise.
For Leibniz, the simplicity and unity of the mind still allows for the multiplicity of perceptions and appetitions. The multiplicity, however, should not only be interpreted as diachronous but also synchronous; that is, the mind despite its simplicity and unity has within it at any time an infinity of different petites perceptions. A human being, in a waking state, is conscious of particular perceptions, but never all. And here we see that Leibniz's doctrine is important, insofar as it offers a contrast to the Cartesian theory of the mind. According to Leibniz, the mind is always active, for there are always perceptions present to it, even if those perceptions are minute and do not rise to such a level that we are cognizant of them. Thus, even in a deep and dreamless sleep, the mind is active, and perceptions are in the mind. Moreover, if Descartes really did advocate the perfect transparency of the mind, then it should be clear that Leibniz allows for a subtler picture of mental contents: there are many things in the mind that are confused and minute and to which we do not always have complete access.
6.6 The Extent of Human Knowledge
Leibniz, however, does not simply disagree with Locke about the nature of the mind and the possibility of innate ideas. It is also Leibniz's contention that human beings are capable of knowledge in a way that Locke had clearly denied. As shown above, Leibniz is convinced that our knowledge of necessary truths has a completely different foundation from that for which Locke argues. Similarly, Leibniz holds that we can have genuine knowledge of the real essences of things, something called into question by Locke. After all, Locke had argued that we ought to admit that “essence” is really just a word that we use to describe “nominal essence,” a set of sortal concepts based upon sensible qualities; we ought not to act as if “essence” means anything about the real or inner constitution of a thing, for we will remain ignorant of that. Leibniz, however, holds that we can know certain things not only about individuals but also about their species and genera. In Book IV of the New Essays, in which Philalethes – the Locke character – gives his critique of the possibility of our certain knowledge about substances qua natural kinds, Theophilus (Leibniz) says, “[L]et me tell you that there are, for example, hundreds of truths that we can be certain of concerning gold, i.e. that body whose inner essence reveals itself through the greatest weight known here on earth, or through the greatest ductility or by other marks. For we can say that the body with the greatest known ductility is also the heaviest of all known bodies” (A VI vi 400/RB 400). Earlier in the New Essays, Leibniz had said that “essence is fundamentally nothing but the possibility of the thing under consideration” (A VI vi 293/RB 293) and “essences are everlasting because they only concern possibilities” (A VI vi 296/RB 296). It would seem, then, that Leibniz has something like the following in mind: experience informs us of a certain consistent set of sensible properties in, for example, gold; that is, a certain set of properties is compossible. And, more important, we ought to be able to assert with certainty that if some object has the greatest ductility, then it also has the greatest weight.
7. Philosophical Theology
Like most of his great contemporaries (Descartes, Spinoza, Malebranche), Leibniz developed a number of arguments for the existence of God. Two of these are presented in condensed versions in the Monadology §§36–45, as a priori and a posteriori arguments (or ontological and cosmological arguments, to borrow Kant's terminology). But they have long histories in Leibniz's thought. Yet, unlike Descartes and Spinoza at least, Leibniz also expended great efforts in explaining and justifying God's justice and benevolence in this world. In other words, Leibniz was keen to answer the problem of evil. His work on this subject led to his thesis, so roundly mocked in Voltaire's Candide, that we live in the best of all possible worlds.
7.1 The Existence of God
7.1.1 The Ontological Argument
Leibniz made an important contribution to the history of the ontological argument. His reflections on this form of argument go back to the 1670s, and we know that he shared his thoughts on this matter with Spinoza when Leibniz visited him on the way to Hanover. According to Leibniz, the argument that Descartes gives implicitly in the Fifth Meditation and explicitly in the First Set of Replies is faulty. Descartes had argued that God is a being having all perfections, existence is a perfection, therefore, God exists. (AT VII 118–19/CSM II 84–85) But, Leibniz thinks, one needs to show that it is possible for such a being to exist, that is, that it is possible for all perfections to co-exist in one being. If this is so, then and only then an ens perfectissimum can be said to exist. In his short essay That a Most Perfect Being Exists (Quod ens perfectissimum existit) from 1676, Leibniz argues just this. He defines a “perfection” as a “simple quality which is positive and absolute, or, which expresses without any limits whatever it does express” (A VI iii 578/SR 101). And with this definition in hand, Leibniz is then able to claim that there can be no inconsistency among perfections, since a perfection, in being simple and positive, is unanalyzable and incapable of being enclosed by limits. That is, if A and B are perfections, then the proposition “A and B are incompatible” cannot be demonstrated because A and B are simples, nor can the proposition be known per se. Therefore, it is possible that any and all perfections are in fact compatible. And, therefore, Leibniz reasons, a subject of all perfections, or an ens perfectissimum, is indeed possible.
But this argument by itself is not sufficient to determine that God necessarily exists. Leibniz must also show that existence is itself a perfection, so that a being having all perfections, an ens perfectissimum, may be said to exist. More exactly, Leibniz needs to show that necessary existence belongs to the essence of God. And this he does in another short piece from this period, writing “Again, a necessary being is the same as a being from whose essence existence follows. For a necessary being is one which necessarily exists, such that for it not to exist would imply a contradiction, and so would conflict with the concept or essence of this being” (A VI iii 583/SR 107). In other words, if it is the case that a necessary being is the same thing as a being whose existence follows from its essence, then existence must in fact be one of its essential properties. Leibniz continues in this short reflection, “And so existence belongs to its concept or essence. From this we have a splendid theorem, which is the pinnacle of modal theory and by which one moves in a wonderful way from potentiality to act: If a necessary being is possible, it follows that it exists actually, or, that such a being is actually found in the universe” (A VI iii 583/SR 107). The “pinnacle of Modal Theory” that Leibniz mentions here is none other than one of the notorious axioms of the modal logic S5: ◊□p → □p. In short, Leibniz's argument is the following:
(1) God is a being having all perfections. (Definition) (2) A perfection is a simple and absolute property. (Definition) (3) Existence is a perfection. (4) If existence is part of the essence of a thing, then it is a necessary being. (5) If it is possible for a necessary being to exist, then a necessary being does exist. (6) It is possible for a being to have all perfections. (7) Therefore, a necessary being (God) does exist.
It should be noted that Leibniz's argument bears a certain affinity with the ontological argument that Gödel gives, insofar as it also seeks to demonstrate the possibility of a being having all simple, positive properties. (For Gödel's argument, see the entry on ontological arguments.)
7.1.2 The Cosmological Argument
As we have seen, the Principle of Sufficient Reason is one of the bedrock principles of all of Leibniz's philosophy. In the Monadology, Leibniz appeals to PSR, saying that even in the case of contingent truths or truths of fact there must be a sufficient reason why they are so and not otherwise. (Monadology §36) But, since each particular truth of fact is contingent upon some other (prior) truth of fact, the reason for the entire series of truths must be located outside the series, and this ultimate reason is what we call God. (Monadology §37)
In the Theodicy, Leibniz fills out this argument with a fascinating account of the nature of God. First, insofar as the first cause of the entire series must have been able to survey all other possible worlds, it has understanding. Second, insofar as it was able to select one world among the infinity of possible worlds, it has a will. Third, insofar as it was able to bring about this world, it has power. (Leibniz adds here that “power relates to being, wisdom or understanding to truth, and will to good.”) Fourth, insofar as the first cause relates to all possibles, its understanding, will and power are infinite. And, fifth, insofar as everything is connected together, there is no reason to suppose more than one God. Thus, Leibniz is able to demonstrate the uniqueness of God, his omniscience, omnipotence, and benevolence from the twin assumptions of the contingency of the world and the Principle of Sufficient Reason. (Theodicy §7: G VI 106–07/H 127–28) Naturally, if one were deny the existence of possible worlds in the sense conceived by Leibniz or deny PSR (by, say, admitting “brute facts”), then one would hardly be moved by this kind of argument.
7.2 Optimism
Leibniz's account of the nature of possible worlds is dealt with in a separate entry. Here the following simple question will be addressed: How can this world be the best of all possible worlds? After all, as Voltaire brought out so clearly in Candide, it certainly seems that this world, in which one finds no short supply of natural and moral horrors, is far from perfect – indeed, it seems pretty lousy. Certainly only a fool could believe that it is the best world possible. But, Leibniz speaks on behalf of the fool, with an argument that has essentially the following structure:
(1) God is omnipotent and omniscient and benevolent and the free creator of the world. (Definition) (2) Things could have been otherwise–i.e., there are other possible worlds. (Premise) (3) Suppose this world is not the best of all possible worlds. (I.e., “The world could be better.”) (4) If this world is not the best of all possible worlds, then at least one of the following must be the case:
- God was not powerful enough to bring about a better world; or
- God did not know how this world would develop after his creation of it (i.e. God lacked foreknowledge); or
- God did not wish this world to be the best; or
- God did not create the world; or
- there were no other possible worlds from which God could choose.
(5) But, any one or more of the disjuncts of (4) contradicts (1) or (2). (6) Therefore, this world is the best of all possible worlds.
In other words, Leibniz seems to argue that, if one is to hold the traditional theistic conception of God and believe that one can meaningfully assert that the world could have been other than it is, then one must hold that this world is the best possible. Naturally, this argument is simply the Christian retort to the Epicurean argument against theism.
But what are the criteria by which one can say that this world is the best? It should be clear that Leibniz nowhere says that this argument implies that everything has to be wonderful. Indeed, Leibniz is squarely in the tradition of all Christian apologists going back to Augustine, arguing that we cannot have knowledge of the whole of the world and that even if a piece of the mosaic that is discoverable to us is ugly the whole may indeed have great beauty. Still, Leibniz does offer at least two considerations relevant to the determination of the happiness and perfection of the world. He tells us in the Discourse on Metaphysics, first, that “…the happiness of minds is the principal aim of God…” (A VI iv 1537/AG 38) and, second, that “God has chosen the most perfect world, that is, the one which is at the same time the simplest in hypotheses and the richest in phenomena” (A VI iv 1538/AG 39). So, is this world of genocide and natural disaster better than a world containing only one multifoliate rose? Yes, because the former is a world in which an infinity of minds perceive and reflect on the diversity of phenomena caused by a modest number of simple laws. To the more difficult question whether there is a better world with perhaps a little less genocide and natural disaster Leibniz can only respond that, if so, God would have brought it into actuality. And this, of course, is to say that there really is no better possible world.
Bibliography
Primary Sources for Leibniz with Abbreviations
- Confessio Philosophi: Papers Concerning the Problem of Evil, 1671–1678. Translated and edited by Robert C. Sleigh, Jr. New Haven, CT: Yale University Press, 2005. - The Labyrinth of the Continuum: Writings on the Continuum Problem, 1672–1686. Translated and edited by Richard T. W. Arthur. New Haven, CT: Yale University Press, 2002. - The Leibniz-Arnauld Correspondence. Edited and translated by H. T. Mason. Manchester: Manchester University Press, 1967. - The Leibniz-Des Bosses Correspondence. Edited and translated by Brandon C. Look and Donald Rutherford. New Haven, CT: Yale University Press, 2007. - The Leibniz-De Volder Correspondence: With Selections from the Correspondence between Leibniz and Johann Bernoulli. Edited and translated by Paul Lodge. New Haven: Yale University Press, 2013. - Lettres de Leibniz à Arnauld d'après un manuscrit inédit. Edited by Geneviève Rodis-Lewis. Paris: Presses Universitaires de France, 1952. - Logical Papers. Translated and edited by G. H. R. Parkinson. Oxford: Clarendon Press, 1966. [GM] Mathematische Schriften. 7 vols. Edited by C. I. Gerhardt. Halle, 1849–63. Reprint, Hildesheim: Georg Olms, 1963. [RB] New Essays on Human Understanding. Translated by Peter Remnant and Jonathan Bennett. Cambridge: Cambridge University Press, 1981. - Nouvelles lettres et opuscules inédits de Leibniz. Edited by A. Foucher de Careil. Paris, 1857. Reprint, Hildesheim: Georg Olms, 1971. - Opera omnia, nunc primum collecta… 6 vols. Edited by Ludovici Dutens. Genevae, 1768. [C] Opuscules et fragments inédits de Leibniz. Extraits des manuscrits… Edited by Louis Couturat. Paris: Presses Universitaires de France, 1903. Reprint, Hildesheim: Georg Olms, 1961. [AG] Philosophical Essays. Translated and edited by Roger Ariew and Dan Garber. Indianapolis: Hackett, 1989. [L] Philosophical Papers and Letters. Edited and translated by Leroy E. Loemker. 2d ed., Dordrect: D. Reidel, 1969. - Philosophical Texts. Edited and translated by R.S. Woolhouse and Richard Francks. Oxford: Oxford University Press, 1998. [G] Die philosophischen Schriften. 7 vols. Edited by C. I. Gerhardt. Berlin, 1875–90. Reprint, Hildesheim: Georg Olms, 1965. - Political Writings. Edited by Patrick Riley. Second edition. Cambridge: Cambridge University Press, 1988. [A] Sämtliche Schriften und Briefe. Edited by the Deutsche Akademie der Wissenschaften zu Berlin. Darmstadt, 1923 ff., Leipzig, 1938 ff., Berlin, 1950 ff. Cited by Series (Reihe) and Volume (Band). (To date the Akademie edition, Series VI, has the philosophical writings to 1690, plus the New Essays, as well as, in Series II, Leibniz's philosophical correspondence to 1685.) [SR] De Summa Rerum: Metaphysical Paper, 1675–1676. Translated and edited by G.H.R. Parkinson. New Haven, CT: Yale University Press, 1992. - Textes inédits d'après les manuscrits de la Bibliothèque provinciale de Hanovre. 2 vols. Edited by Gaston Grua. Paris: Presses Universitaires de France, 1948. [H] Theodicy: Essays on the Goodness of God, the Freedom on Man and the Origin of Evil. Translated by E. M. Huggard. La Salle, IL: Open Court, 1985.
Other Primary Sources
[CSM] The Philosophical Writings of Descartes. Edited by John Cottingham, Robert Stoothoff, Dugald Murdoch. 2 Volumes. Cambridge: Cambridge University Press, 1984. [AT] Oeuvres de Descartes. Edited by Charles Adam and Paul Tannery. 12 Volumes. Reprint, Paris: J. Vrin, 1996.
Secondary Sources
- Adams, Robert Merrihew, 1972. “Must God Create the Best?” Philosophical Review, 81(3): 317–332.
- –––, 1983. “Phenomenalism and Corporeal Substance in Leibniz,” Midwest Studies in Philosophy, 8(1): 217–257.
- –––, 1984. “Predication, Truth and Transworld Identity in Leibniz,” in Bogen and McGuire, How Things Are, Dordrecht: D. Reidel, 235–283.
- –––, 1994. Leibniz: Determinist, Theist, Idealist, Oxford: Oxford University Press.
- Aiton, Eric, 1985. Leibniz: A Biography, Bristol: Adam Hilger.
- Andrault, Raphaele, 2006. “Leibniz et les iatromécaniciens,” Studia Leibnitiana, 38/39(1): 63–88.
- Antognazza, Maria Rosa, 2008. Leibniz on the Trinity and the Incarnation: Reason and Revelation in the Seventeenth Century, Gerald Parks (trans.), New Haven: Yale University Press.
- –––, 2009. Leibniz: An Intellectual Biography, Cambridge: Cambridge University Press.
- Arthur, Richard, 1985. “Leibniz's Theory of Time,” in Okruhlik and Brown (eds.), The Natural Philosophy of Leibniz, 263–313.
- Beeley, Philip, 1996. Kontinuität und Mechanismus. Stuttgart: Steiner Verlag (Studia Leibnitiana, Supplement 30).
- Bolton, Martha Brandt, 1996. “The Nominalist Argument of the New Essays,” The Leibniz Review, 6: 1–24.
- –––, 1998. “Locke, Leibniz, and the Logic of Mechanism,” Journal of the History of Philosophy, 36 (2): 189–213.
- Broad, C. D., 1975. Leibniz: An Introduction, Cambridge: Cambridge University Press.
- Brown, Gregory, 1987. “Compossibility, Harmony, and Perfection in Leibniz,” The Philosophical Review, 96(2): 173–203.
- –––, 1988. “Leibniz's Theodicy and the Confluence of Worldly Goods,” Journal of the History of Philosophy, 26(4): 571–591
- –––, 1992. “Is There a Pre-Established Harmony of Aggregates in the Leibnizian Dynamics, or Do Non-Substantial Bodies Interact?” Journal of the History of Philosophy, 30(1): 53–75.
- Brown, Stuart, 1984. Leibniz, Minneapolis: University of Minnesota Press.
- Burkhardt, Hans, 1980. Logik und Semiotik in der Philosophie von Leibniz, Munich: Philosophia Verlag.
- Busche, Hubertus, 1997. Leibniz' Weg ins perspektivische Universum, Hamburg: Meiner.
- Cassirer, Ernst, 1902. Leibniz' System in Seinen Wissenschaftlichen Grundlagen, Marburg: Elwert; reprinted Hildesheim: Olms, 1962.
- Coudert, Allison P., 1995. Leibniz and the Kabbalah, Dordrecht: Springer.
- Couturat, Louis, 1901. La logique de Leibniz. Paris: Presses Universitaires de France; reprinted Hildesheim: Georg Olms, 1961.
- Cover, J.A. and J. O'Leary-Hawthorne, 1999. Substance and Individuation in Leibniz, Cambridge: Cambridge University Press.
- Di Bella, Stefano, 2005. The Science of the Individual: Leibniz's Ontology of Individual Substance, Dordrect: Springer.
- Duchesneau, François, 1993. Leibniz et la méthode de la science, Paris: Presses Universitaires de France.
- –––, 1994. La dynamique de Leibniz, Paris: J. Vrin.
- Fichant, Michel, 1998. Science et métaphysique dans Descartes et Leibniz, Paris: Presses Universitaires de France.
- –––, 2003. “Leibniz et les machines de la nature,” Studia Leibnitiana, 35(1): 1–28.
- –––, 2004. “L'Invention métaphysique” (Introduction to Leibniz, Discours de métaphysique suivi de Monadologie et autres textes), Paris: Gallimard, 1–123.
- Frankfurt, Harry G. (ed.), 1972. Leibniz: A Collection of Critical Essays, New York: Doubleday.
- Furth, Montgomery, 1967. “Monadology,” The Philosophical Review, 76(2): 169–200.
- Garber, Daniel, 1982. “Motion and Metaphysics in the Young Leibniz,” in Hooker (ed.) 1982, pp. 160–184.
- –––, 1983. “Mind, Body and the Laws of Nature in Descartes and Leibniz,“Midwest Studies in Philosophy, 8(1): 105–133.
- –––, 1985. “Leibniz and the Foundations of Physics: The Middle Years,” in Okrulik and Brown, Natural Philosophy, 27–130.
- –––, 2009. Leibniz: Body, Substance, Monad, New York and Oxford: Oxford University Press.
- Gaudemar, Martine de, 1994. Leibniz: de la puissance au sujet, Paris: Vrin.
- Goldenbaum, Ursula, and Douglas Jesseph (eds.), 2008. Infinitesimal Differences: Controversies between Leibniz and his Contemporaries, Berlin: De Gruyter.
- Guéroult, Martial, 1967. Leibniz: Dynamique et Métaphysique. Paris: Aubier.
- Hacking, Ian, 1972. “Individual Substance,” in H. Frankfurt (ed.), Leibniz: A Collection of Critical Essays, New York: Doubleday, 137–153.
- Hartz, Glenn, 2006. Leibniz's Final System, New York: Routledge.
- Hooker, Michael (ed.), 1982. Leibniz: Critical and Interpretive Essays, Minneapolis: University of Minnesota Press.
- Ishiguro, Hidé, 1990. Leibniz's Philosophy of Logic and Language, 2nd ed., Cambridge: Cambridge University Press.
- –––, 1972. “Leibniz's Theory of the Ideality of Relations,” in Frankfurt, Leibniz: A Collection of Critical Essays, New York: Doubleday, 191–213.
- Jalabert, Jacques, 1947. La théorie leibnizienne de la substance, Paris: Presses Universitaires de France.
- –––, 1960. Le Dieu de Leibniz, Paris: Presses Universitaires de France.
- Jauernig, Anja, 2008. “The Modal Strength of Leibniz's Principle of the Identity of Indiscernibles,” Oxford Studies in Early Modern Philosophy, IV: 191–225.
- –––, 2010. “Disentangling Leibniz's Views on Relations and Extrinsic Denominations,” Journal of the History of Philosophy, 48 (2): 171–205.
- Jolley, Nicholas, 1984. Leibniz and Locke: A Study of the “New Essays on Human Understanding,” Oxford: Clarendon Press.
- –––, 1986. “Leibniz and Phenomenalism,” Studia Leibnitiana, XVIII(1): 38–51.
- –––, 2005. Leibniz, New York: Routledge.
- Jolley, Nicholas (ed.), 1995. The Cambridge Companion to Leibniz, Cambridge: Cambridge University Press.
- Kauppi, Raili, 1960. Über die Leibnizsche Logik, Helsinki: Acta Philosophica Fennica, Fasc. XII.
- Kulstad, Mark A., 1980. “A Closer Look at Leibniz's Alleged Reduction of Relations,” Southern Journal of Philosophy, 18(4): 417–32.
- –––, 1991. Leibniz on Apperception, Consciousness and Reflection, Munich: Philosophia Verlag.
- –––, 1993. “Two Interpretations of the Pre-Established Harmony in the Philosophy of Leibniz,” Synthese, 96(3): 477–504.
- Lærke, Mogens, 2008. Leibniz et Spinoza: le genèse d'une opposition complexe, Paris: Honoré Champion.
- –––, 2011. “Leibniz's Cosmological Argument for the Existence of God,” Archiv für Geschichte der Philosophie, 93(1): 58–84.
- Leduc, Christian, 2009. Substance, individu et connaissance chez Leibniz, Montreal: University of Montreal Press.
- Levey, Samuel, 1998. “Leibniz on Mathematics and the Actually Infinite Division of Matter,” Philosophical Review, 107(1): 49–96.
- Lin, Martin, 2012. “Rationalism and Necessitarianism,” Noûs, 46(3): 418–448.
- Lodge, Paul, 1998a. “Leibniz's Heterogeneity Argument against the Cartesian Conception of Body,” Studia Leibnitiana, 30(1): 83–102.
- –––, 1998b. “Leibniz's Commitment to the Pre-established Harmony in the Late 1670s and Early 1680s,” Archiv für Geschichte der Philosophie, 80(3): 292–320.
- –––, 2001. “Leibniz's Notion of an Aggregate,” British Journal for the History of Philosophy, 9(3): 467–486.
- Lodge, Paul (ed.), 2004. Leibniz and His Correspondents, Cambridge: Cambridge University Press.
- Lodge, Paul, and Marc Bobro, 1998. “Stepping Back Inside Leibniz's Mill,” The Monist, 81(4): 553–572.
- Look, Brandon C., 1999. Leibniz and the ‘Vinculum Substantiale’, Stuttgart: Steiner (Studia Leibnitiana, Supplement 30).
- –––, 2002. “On Monadic Domination in Leibniz's Metaphysics,” British Journal for the History of Philosophy, 10(3): 379–399.
- –––, 2005. “Leibniz and the Shelf of Essence,” The Leibniz Review, 15: 27–47.
- –––, 2010. “Leibniz's Metaphysics and Metametaphysics: Idealism, Realism and the Nature of Substance,” Philosophy Compass, 5(11): 871–879.
- Look, Brandon C. (ed.), 2011. The Continuum Companion to Leibniz, London: Continuum.
- Martin, Gottfried, 1964. Leibniz: Logic and Metaphysics, Manchester: Manchester University Press.
- Mates, Benson, 1972. “Individuals and Modality in the Philosophy of Leibniz,” Studia Leibnitiana, IV(2): 81–118.
- –––, 1986. The Philosophy of Leibniz: Metaphysics and Language, Oxford: Oxford University Press.
- McDonough, Jeffrey K., 2008. “Leibniz's Two Realms Revisited,” Noûs, 42(4): 673–696.
- McRae, Robert, 1976. Leibniz: Perception, Apperception, and Thought, Toronto: University of Toronto Press.
- Mercer, Christia, 2001. Leibniz's Metaphysics: Its Origin and Development, Cambridge: Cambridge University Press.
- Mercer, Christia, and Robert C. Sleigh Jr., 1995. “Metaphysics: The early period to the Discourse on Metaphysics,” in N. Jolley (ed.), The Cambridge Companion to Leibniz, 67–123.
- Mondadori, Fabrizio, 1973. “Reference, Essentialism, and Modality in Leibniz's Metaphysics,” Studia Leibnitiana, V(1): 74–101.
- –––, 1985. “Understanding Superessentialism,” Studia Leibnitiana, XVII(2): 162–190.
- Mugnai, Massimo, 1992. Leibniz' Theory of Relations, Stuttgart: Franz Steiner (Studia Leibnitiana, Supplement 28).
- Nachtomy, Ohad, 2007. Possibility, Agency, and Individuality in Leibniz's Metaphysics, Dordrecht: Springer.
- Newlands, Samuel, 2010. “The Harmony of Spinoza and Leibniz,” Philosophy and Phenomenological Research, 81(1): 64–104.
- Okruhlik, Kathleen, and James Brown (eds.), 1985. The Natural Philosophy of Leibniz, Dordrecht: D. Reidel.
- Parkinson, G. H. R., 1965. Logic and Reality in Leibniz's Metaphysics, Oxford: Oxford University Press.
- Phemister, Pauline, 2001. “Corporeal Substances and the ‘Discourse on Metaphysics’,” Studia Leibnitiana, 33 (1): 68–85.
- –––, 2005. Leibniz and the Natural World: Activity, Passivity, and Corporeal Substances in Leibniz's Philosophy, Dordrecht: Springer.
- Picon, Marine, 2003. “Vers la doctrine de l'entendement en abrégé: éléments pour une généalogie des Meditationes de cognitione, veritate, et ideis,” Studia Leibnitiana, 35 (1): 102–132.
- Puryear, Stephen, 2010. “Monadic Interaction,” British Journal for the History of Philosophy, 18(5): 763–796.
- Rateau, Paul, 2008. La question du mal chez Leibniz, Paris: Champion.
- Rauzy, Jean-Baptiste, 2001. La doctrine leibnizienne de la vérité: aspects logiques et ontologiques, Paris: J. Vrin.
- Rescher, Nicholas, 1979. Leibniz: An Introduction to His Philosophy, Oxford: Basil Blackwell.
- –––, 1981. Leibniz's Metaphysics of Nature, Dordrecht: D. Reidel.
- –––, 1967. The Philosophy of Leibniz, Englewood Cliffs, NJ: Prentice Hall.
- Rescher, Nicholas (ed.), 1989. Leibnizian Inquiries: A Group of Essays, New York: University Press of America.
- Rey, Anne-Lise, 2011. “Les paradoxes de la singularité: infini et perception chez GW Leibniz,” Revue de métaphysique et de morale, 70(2): 253–266.
- Riley, Patrick, 1996. Leibniz' Universal Jurisprudence: Justice as Charity of the Wise, Cambridge, MA: Harvard University Press.
- Risi, Vincenzo de, 2007. Geometry and Monadology: Leibniz's Analysis Situs and Philosophy of Space, Basel: Birkhäuser.
- Robinet, André, 1986. Architectonique Disjonctive Automates Systémiques et Idéalité Transcendantale dans l'Œuvre de G.W. Leibniz, Paris: J. Vrin.
- Rodriguez-Pereyra, Gonzalo, 1999. “Leibniz's argument for the identity of indiscernibles in his correspondence with Clarke,” Australasian Journal of Philosophy, 77(4): 429–438.
- Roland, Jeanne, 2012. Leibniz et l'individualité organique, Montreal: University of Montreal Press.
- Russell, Bertrand, 1937. A Critical Exposition of the Philosophy of Leibniz, 2nd ed., London: Allen & Unwin.
- Rutherford, Donald, 1990a. “Leibniz's ‘Analysis of Multitude and Phenomena into Unities and Reality,’” Journal of the History of Philosophy, 28: 525–552.
- –––, 1990b. “Phenomenalism and the Reality of Body in Leibniz's Later Philosophy,” Studia Leibnitiana, XXII(1): 11–28.
- –––, 1993. “Natures, Laws, and Miracles: The Roots of Leibniz's Critique of Occasionalism,” in Steven Nadler (ed.), Causation in Early Modern Philosophy, College Park, PA: Pennsylvania State University Press, 135–58.
- –––, 1994. “Leibniz and the Problem of Monadic Aggregation,” Archiv für Geschichte der Philosophie, 76(1): 65–90.
- –––, 1995a. Leibniz and the Rational Order of Nature, Cambridge: Cambridge University Press.
- –––, 1995b. “Metaphysics: The late period,” in N. Jolley (ed.), The Cambridge Companion to Leibniz, Cambridge: Cambridge University Press, 124–174.
- –––, 2008. “Leibniz as Idealist,” Oxford Studies in Early Modern Philosophy, IV: 141–190.
- Schepers, Heinrich, 1965. “Zum Problem der Kontingenz bei Leibniz: Die beste der möglichen Welten,” in Collegium Philosophicum: Joachim Ritter zum 60. Geburtstag, Basel and Stuttgart: Schwabe, 326–350.
- Sellers, Wilfrid, 1965. “Meditations Leibniziennes,” American Philosophical Quarterly, 2(2): 105–118.
- Simmons, Alison, 2001. “Changing the Cartesian Mind: Leibniz on Sensation, Representation and Consciousness,” Philosophical Review, 110(1): 31–75.
- Sleigh, R. C., Jr., 1982. “Truth and Sufficient Reason in the Philosophy of Leibniz,” in Hooker (ed.), 1982, 209–42.
- –––, 1983a. “Expression, Perception and Harmony in the Discourse,” Southern Journal of Philosophy, 21 (Supplement): 71–84.
- –––, 1983b. “Leibniz on the Two Great Principles of All Our Reasonings,” Midwest Studies in Philosophy, 8(1): 193–217.
- –––, 1990a. Leibniz and Arnauld: A Commentary on Their Correspondence, New Haven: Yale University Press.
- –––, 1990b. “Leibniz on Malebranche on Causality,” in J.A. Cover and M. Kulstad (eds.), Central Themes in Early Modern Philosophy, Indianapolis: Hackett, 161–193.
- Smith, Justin E. H., 2004. “Christian Platonism and the Metaphysics of Body in Leibniz,” British Journal for the History of Philosophy, 12(1): 43–59.
- –––, 2010. Divine Machines: Leibniz and the Sciences of Life, Princeton: Princeton University Press.
- Smith, Justin E. H. and Ohad Nachtomy (eds.), 2011. Machines of Nature and Corporeal Substances In Leibniz, Dordrecht: Springer, 2011.
- Wilson, Catherine, 1983. “Leibnizian Optimism,” The Journal of Philosophy, 80 (11): 765–783.
- –––, 1987. “De Ipsa Natura: Sources of Leibniz's Doctrines of Force, Activity and Natural Law” Studia Leibnitiana, 19(2): 148–172.
- –––, 1989. Leibniz's Metaphysics: A Historical and Comparative Study, Manchester: Manchester University Press.
- –––, 2000. “Plenitude and Compossibility in Leibniz,” The Leibniz Review, 10: 1–20.
- Wilson, Margaret D., 1976. “Leibniz's Dynamics and Contingency in Nature,” in Machamer and Turnbull, Motion and Time, Space and Matter, London: Routledge, 264–289; reprinted in Wilson 1999.
- –––, 1978/9. “Possible Gods,” Review of Metaphysics, 32(4): 717–733; reprinted in Wilson 1999.
- –––, 1987. “The Phenomenalisms of Leibniz and Berkeley,” in Essays on the Philosophy of George Berkeley, E. Sosa (ed.), Dordrecht: D. Reidel, 3–22; reprinted in Wilson 1999.
- –––, 1999. Ideas and Mechanism: Essays on Early Modern Philosophy, Princeton: Princeton University Press.
- Woolhouse, R. S., 1993. Descartes, Spinoza, Leibniz: The Concept of Substance in Seventeenth Century Metaphysics, Routledge: New York.
- Zalta, Edward, 2000. “A (Leibnizian) Theory of Concepts,” Philosophiegeschichte und logische Analyse / Logical Analysis and History of Philosophy, 3: 137–183.
Academic Tools
How to cite this entry. Preview the PDF version of this entry at the Friends of the SEP Society. Look up this entry topic at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers, with links to its database.
Other Internet Resources
- Gallica (Contains searchable texts from Leibniz)
- Gottfried-Wilhelm-Leibniz-Gesellschaft
- Leibnitiana
- Leibniz-Edition
- Leibniz-Forschungsstelle
- Leibniz – online texts, links to a variety of online texts by Leibniz, maintained by Clinton Tolley (Philosophy, UCSD).
- MacTutor page on Leibniz, including a picture of a model of Leibniz's calculating machine
Acknowledgments
The editors would like to thank Sally Ferguson for noticing inaccuracies in a claim and in a quote attributed to Leibniz.






 Sophie-Charlotte de Hanovre.
Sophie-Charlotte de Hanovre.




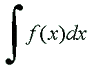





:max_bytes(150000):strip_icc():format(webp)/Gottfried_Wilhelm_Leibniz_c1700-56a2ee155f9b58b7d0cfc7e7.jpg)
:max_bytes(150000):strip_icc():format(webp)/higher-learning-548777197-2e1d8af3a3d748c59673b65e19b506ea.jpg)
:max_bytes(150000):strip_icc():format(webp)/claudiodivizia-GottfriedLeibniz-5c770de746e0fb0001edc779.jpg)